AlphaPoke: can an AI learn how to play Pokémon?

For the "Sistemi Intelligenti Avanzati" course erogated by Università degli Studi di Milano I had to create a project using AI techniques. I chose to use this opportunity to try to answer a simple question: is it possible to train an artificial intelligence to play competitive Pokémon?
Disclamer: the following article aims to give a high-level explanation of the project, wihout all the complex formulas and formalisms. For more information read the report or explore the source code.
The game
The project was created using Pokémon Gen 8 rules (VGC 2020, VGC 2021, VGC 2022) but considering only single battles and not double battles. For those of you that do not know Pokémon's rules (I'm sorry) I advise you to read chapter 2 of my exam report where rules and the gameplay loop are explained.

A screenshot of "Pokémon Sword/Shield" Copyright © Nintendo
The problem
At a first glance Pokémon doesn't seem like an extremely complex game:
- Every player has 6 Pokémon
- Every Pokémon has 4 moves
This does not seem like a "permutation hell". What is unfortunately often ignored in Pokémon is the fact it's highly base on stochastic (random) components and where players have incomplete information (see chapter 3 of the report).
Variables
6 Pokémon e 4 moves per Pokémon. Not a lot, right? Sure, unless you start considering the fact that a Pokémon is defined by:
- its base stats
6 values per Pokémon - its types
- its abilities
- its item
- its stat boosts
- its status condition
- its moves
- its eventual mega evolutions, Z-Moves, Gigamax
- its IV and EV
and that every move is defined by:
- its accuracy
- its base power
- its type
- how many times it hits
- evntual secondary effects
and that the environment is defined by:
- its weather condition
- its field
- its side conditions (Stealth Rock, Toxic Spikes, etc)
RNGesus

What is under the domain of RNGesus? Almost everything:
- Critical hits
- Moves accuracy
- Damage multiplier (every move's damage is rescaled with a multiplier between 0.85 and 1)
- Moves secodary effects
- Multi-hit moves (for example Fury Attack, Rock Blast, etc.)
All of this makes finding the optimal policy (for those not in the field: a policy specifies what action the agent needs to choose in a specific state) extremely difficult as an action applied different times to the same state leads to different results.
Information
As if it wasn't enough, Pokémon is a game with incomplete information. This means that an agent has to decide what action to execute without fully knowing the environment (obvious example: opponent's Pokémon and their movesets).
First approach: Q-Learning
First attepts at reinforcement learning weren't based on neural networks but on huge state-action tables and on the assumption that the game is a markovian process (Pokémon satisfies that assumption). Those are a lot of words: let's go step-by-step.
A markovian process is a dynamic system where the transition probabilities from a state to another depend only on the previous state and not the state history (simple example: it doesn't matter whether a state is reached using Harden twice or using Iron Defense once, the transition probabilities from a supereffective move from an opponent Pokémon just switched in is the same).
Reinforcement learning is one of the 3 main categories of automatic learning, in particular this one handles sequential decisions. This technique is based on the same principle that allows us to train conditioned reflexes in animals (see Ivan Pavlov's experiments): the agent receives a reward for every correct choice and a punishment for every wrong one.
The objective of Q-Learning algorithms is to estimate
On-policy learning: SARSA
SARSA (state-action-reward-state-action) reinforcement learning algorithm estimates values of
where
What's
What if two actions have the same value? That is an implementation choice: choose on randomly, take the first one index-wise, etc. The important thing is being consistent.
How do you learn if you always choose the same action that gives a reward?
This is a problem decribed by experts as the pair exploration-exploitation.
Exploration should be prevalent in the beginning of the learning process, when you know almost nothing about the environment.
On the other hand exploitation should be prevalent (but not exclusive) near the end of the training process, when the environment is known.
Often a
Off-policy learning: Q-Learning
The Q-Learning algorithm is similar to SARSA. The only difference lies in the expected future rewards calculation:
As shown in the formulas above, SARSA computes future rewards directly on the learned policy
Learning structure
In general a training step of an agent with this first approach follows this loop (after a fisrt initialization step):
- Agent receives current state
- Agent chooses action
- Agent executes action
- Agent updates its estimate
- Agent updates current state
It is possible to prove that these algorithms guarantee to get in finite time
Limitations of this approach
The biggest limitation of this approach is also the most intuitive: with an highly variable environment, the number of possible states is exponential. This leads to an agent not recognizing two equal states that differ only in a single variable and so an explosion in the state-action table of the policy occurs.
Second approach: DQN (Deep Q-Learning)
To overcome the limitations of state-action tables neural networks are used.
A neural network emulates what happens in the neurons of our brains, so it can generalize similar states: they can estimate
In practice
What actually happens in practice? Even though programmers love using big words in order to look like an elf wizard casting a spell in draconic, DQN works just like Q-Learning but replaces the state-action table with a neural network:
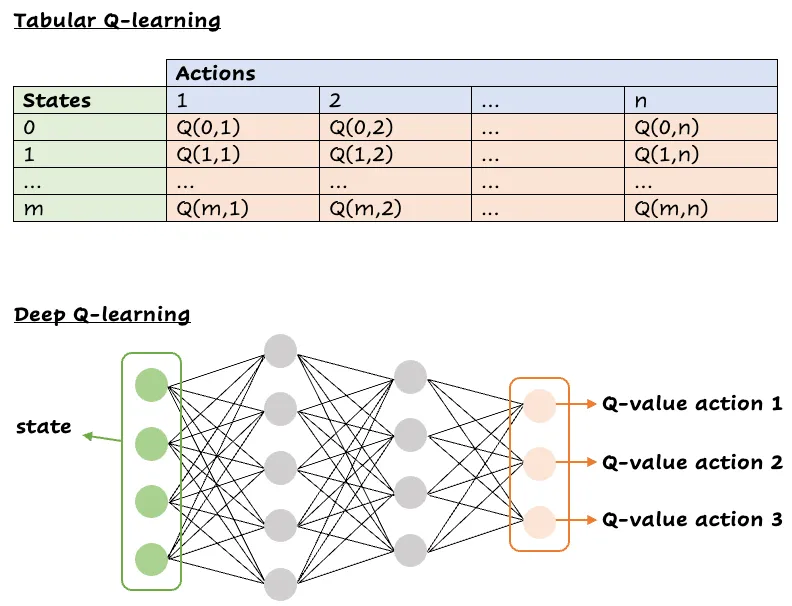
Visual comparison between a state-action table (above) and a neural network for DQN (below)
All the training steps are the same:
- Agent receives current state
- Agent chooses action
- Agent executes action
- Agent updates its estimate
- Agent updates current state
Experimental results
Does this work? In order to answer this question a first step is to know what agents were trained.
Trained agents
Two agents were trained: one using Q-Learning with a state-action table and one with DQN.
Action space
The action space is the set of actions the agent can try to execture in every state and is the same for both agents.
It is the maximal set (not every action is available in every state. In that case a reward of
- Use move
- Use move
- Mega evolve Pokémon and use move
- Dynamax Pokémon and use move
- Switch current Pokémon with the one in the bag in position
In total at most 21 moves are possible while in any state.
State space
The state space represents the encoding of the environment the agent expects.
Disclamer: as both agents were trained in the context of a university project a secondary objective was to reduce the computational cost so they could be trained on a low-end machine. I am aware of the fact that they extremely are sub-otpimal.
Q-Learning
In order to limit the maximum size of the state-action table a single tuple is used:
- An integer between -2 and 2 to represent the balance between the Pokémons' base stats
- An integer between -1 and 1 to represent the balance between the Pokémons' types
- An integer between -1 and 1 to represent the balance between the Pokémons' stat boosts
- A flag to represent whether the opponent's Pokémon is dynamaxed
- A flag to represent whether the agent has to send out another Pokémon (forced switch)
- Four integers between -7 and 3 to represent the value of the moves in the context of the battle based on the move's type, its base power and eventual stat boosts
DQN
The neural network takes as input the encoding of the state. In particular a vector of numerical values. In order to avoid unwanted orderings one-hot encoding is used.
What do you mean with unwanted ordering? Let's take as an example an encoding that maps a Pokémon types into a pair of integers. This could lead the network to think that there is a hierarchy of some kind based on the values the encoding assigns to each type. This issue is avoided using a vector of binary values of length equal to the number of elements to encode and by setting to 1 only the correct one (one-hot).
Neural network
The neural network, just as the state-action-table, was sized with a low-end machine in mind. In order to do so, a single hidden layer with 1024 nodes is used. The output layer has a forced size (21 nodes, the same as the action space size).
Training
Both agents were trained on thousands of simulated matches against heuristics agents in order to get a similar result to a new Pokémon player (e.g. an agent that uses the move with the highest base power, no matter the type).
Results
A first important result is that both agents have a winrate (ratio between won matches and played matches) greter than 50% against completely random agents. This means that probably these agents would have done a better job than most parents when, crying, we asked them to defeat Brock as we picked Charmander as our starter and training it to level 13 so it could learn Metal Claw was too much work for our 9-year-old selves.
A second test was putting them against human players on Pokémon Showdown together with more advanced heuristics (Simple heuristics) and agents that use the most powerful move (Max base power). Unfortunately in this second case results are far less positive (both for the agents and for the humans). The following plots show the mean and peak elo (a value that represents how "good" a player is in a videogame and that is used to match players of similar strength) of each agent during the test (1000 mathces for agent).
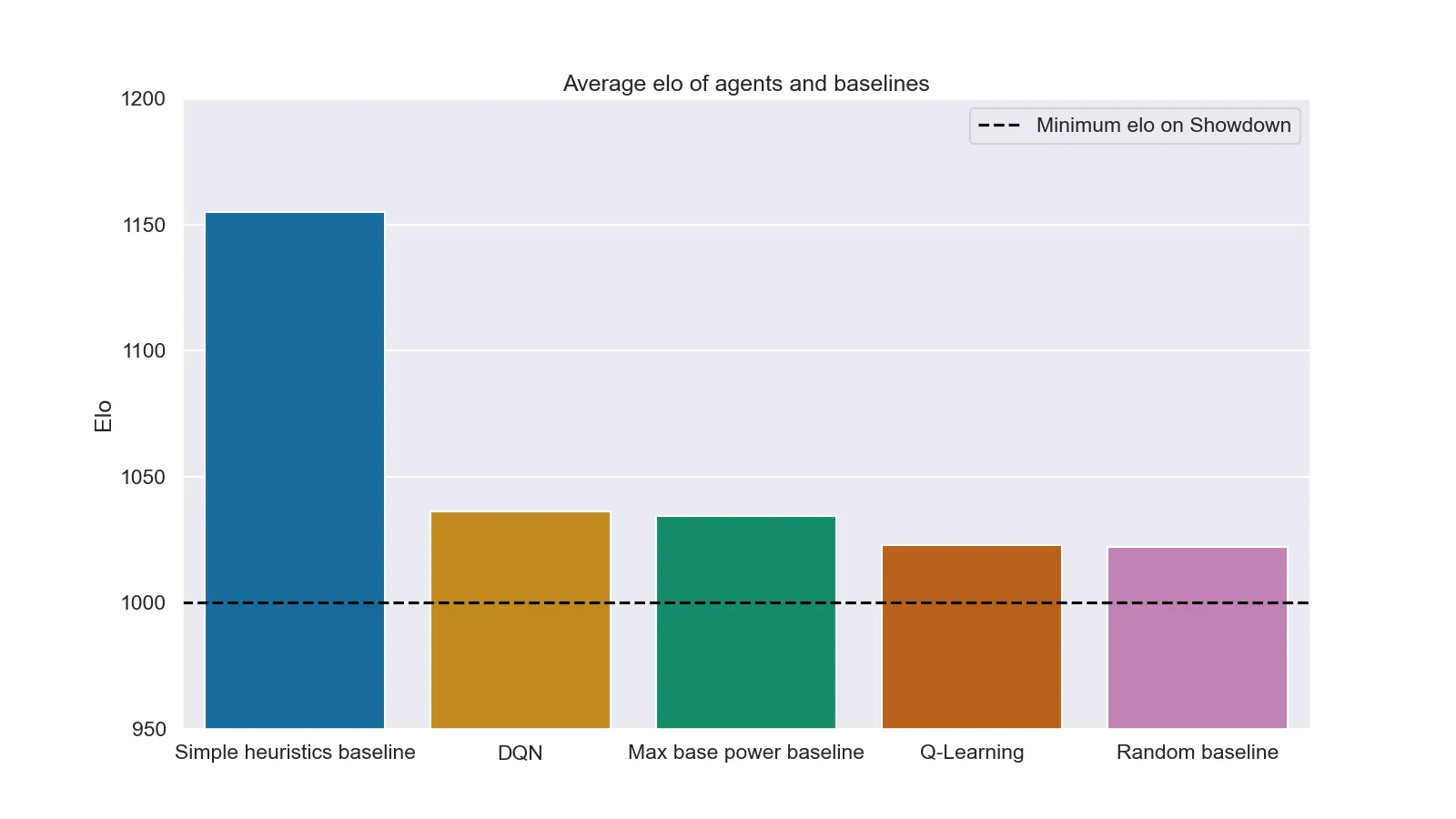
Mean elo of each agent after 1000 matches
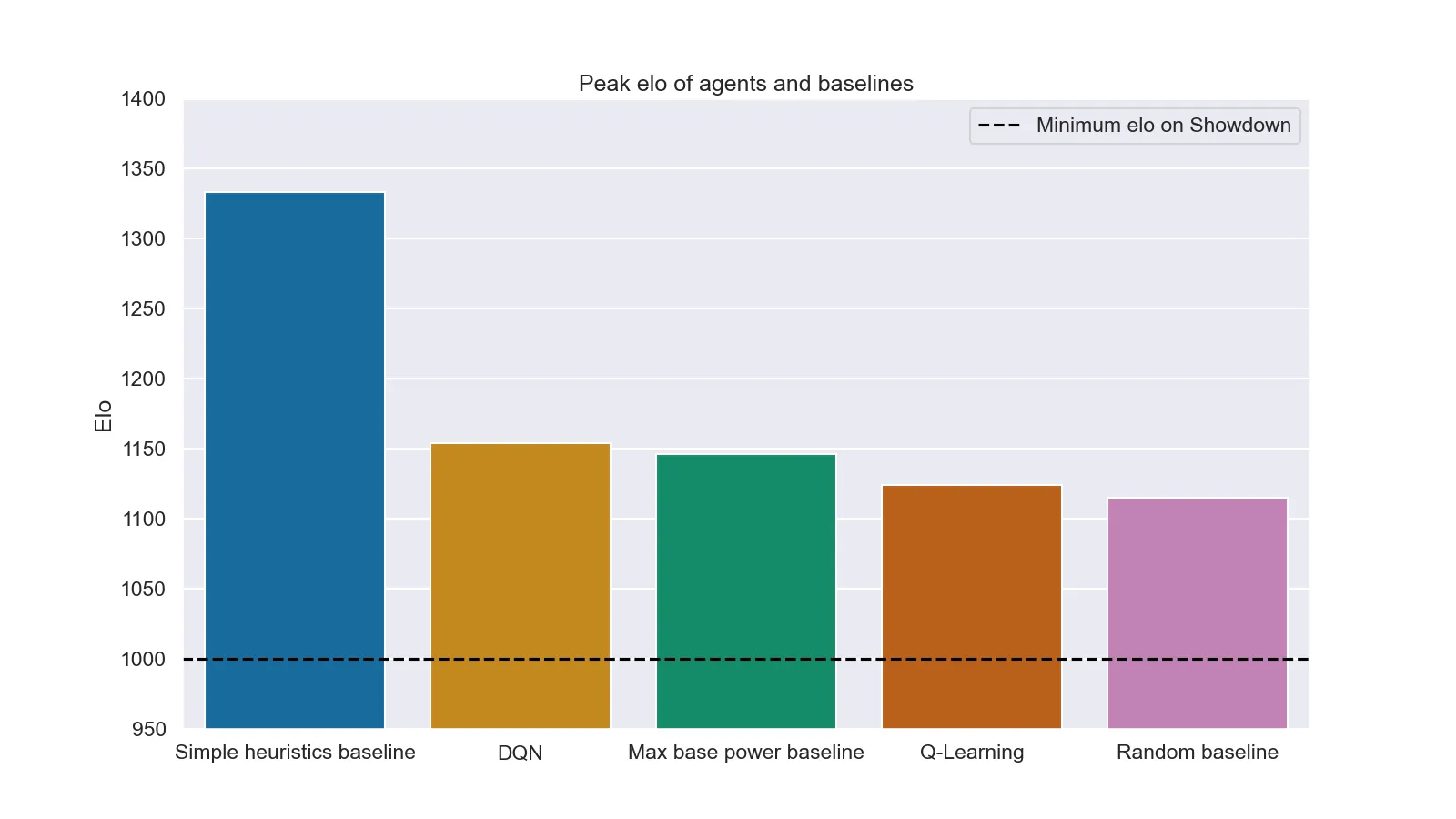
Peak elo of each agent after 1000 matches
It is interesting to note how even a DQN could not beat the result of simple heuristics (this is probably caused by the excessive simplification of the neural network. With a more powerful machine it would have been possible to test more complex architectures, probably leading to a very different result).
Another interesting point is in the random baseline result: a peak elo of around 1125 means that a non-negligible number of people managed to lose against an agent that literally smashes its head on the keyboard and presses random buttons.
For a last consideration we need another plot: the timeline of the trained agents' elos.
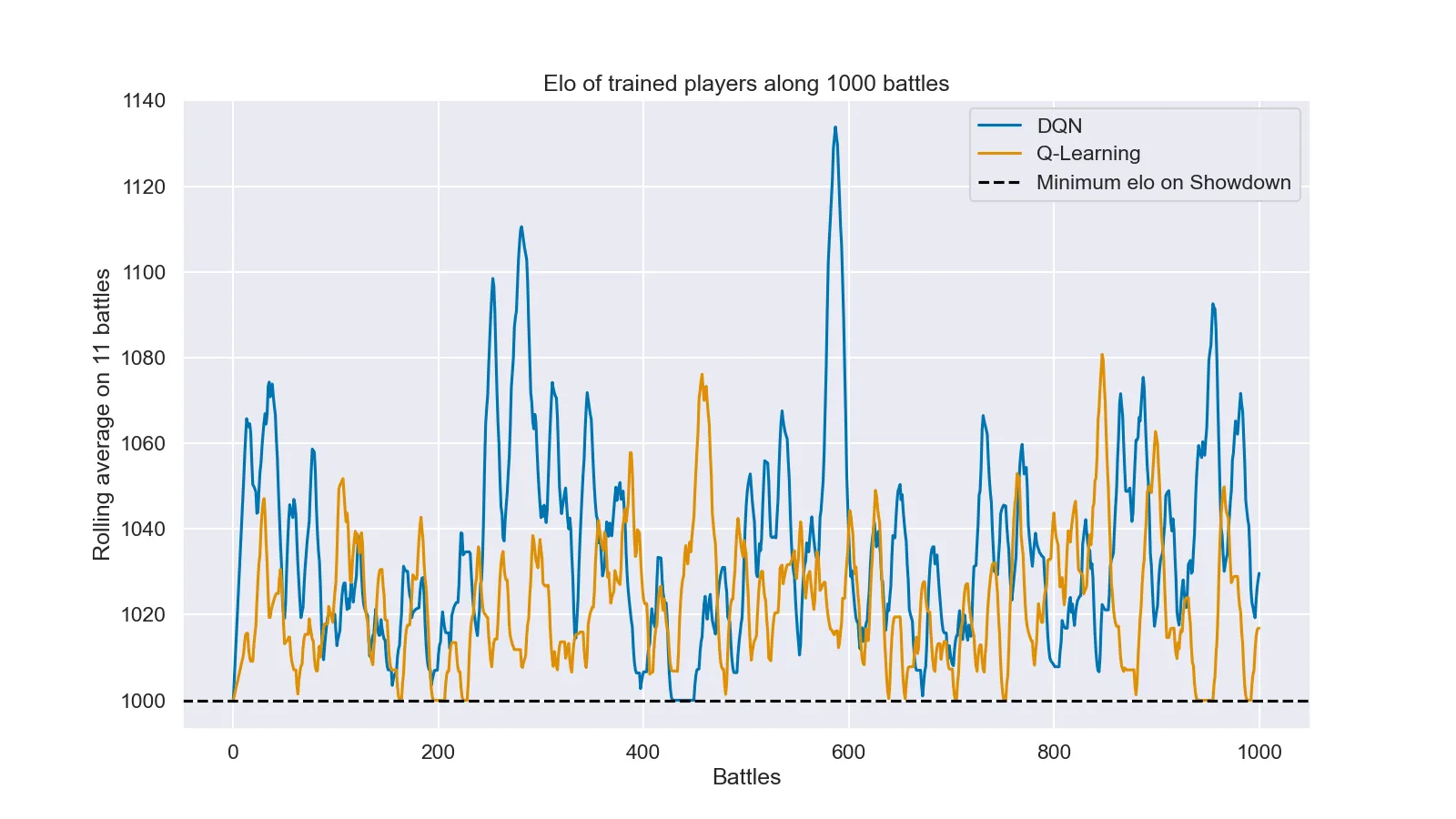
Elo timeline of the two trained agents during 1000 matches
In this plot it is possible to note that none of the agents managed to stabilize around a elo greater than the minimum (1000), even though it seems like without this floor the DQN agent would have managed to stay around 1020, which is almost nothing but still better than the Q-Learning agent.
Can I try them?
Sure. You can find executables for different operative systems here. You only have to follow the instructions written here. In case you were still curious or you wanted to train new agents starting from this project, you may find all the source code here.